류동균의 R 공부방입니다.
선형회귀 분석(Linear regression analysis) 본문
머신러닝을 공부하면서 선형회귀분석(Linear regression analysis)라는 개념을 필수적으로 본적이 있을것이다.
오늘은 이 선형회귀분석의 기초적인 개념에 대해 공부해 보려고 한다.
우선 선형회귀의 개념은 간단하게 머신러닝을 공부하면서 선형회귀분석(Linear regression analysis)라는 개념을 필수적으로 본적이 있을것이다.
오늘은 이 선형회귀분석의 기초적인 개념에 대해 공부해 보려고 한다.
그에 앞서 알아둬야 할 점이 있다. 인공지능으로 데이터의 모델을 구하는데 있어서의 한계가 있다.
머신러닝이라는 것이 전지전능한 인공지능이 아니라 데이터에 의존을 하기 때문에 데이터에 따라서 model은 계속해서 바뀔 수가 있다.
우선 선형회귀분석의 개념은 간단하게 선형 즉 1차함수의 성격을 띄는 데이터들을 1차함수 모델을 만들어 값을 예측하는 것이다.
R에서 기본으로 제공하는 데이터 중에 cars라는 데이터가 있다. 이는 자동차의 속도와 제동거리 두가지 컬럼이 있는데 이 데이터로 선형회귀분석의 기초를 공부해보자.
우선 cars의 데이터를 보기위해 다음과같이 실행해보자
data(cars)
cars
plot(cars)
다음과 같은 그래프가 나올텐대 육안으로 볼때도 speed와 dist가 양의 상관관계를 가진 선형을 띈다고 볼 수 있다.
그러면 이제 speed에 따른 dist를 예측하기위해 Linear model을 만들어보자.
R에서의 선형회귀함수를 얻기위해서는 Linear model -> lm()이라는 함수가 사용된다.
#linear model
# lm("종속변수" ~ "독립변수",Data)
# 종속변수 = 쉽게 말해서 Y
# 독립변수 = 쉽게 말해서 x
lm_model <- lm(dist ~ speed, cars)

lm_model을 실행시키면 다음과 같은 결과가 나올것이다. Intercept는 1차식에서의 y절편 speed는 기울기를 나타낸다.
그럼 위의 자료를 근거로 우리는 y= 3.932x - 17.579라는 1차식을 세울 수가 있다.
# 예측
fitted(lm_model)
# 실측값
cars$dist
# 잔차
residuals(lm_model)
#신뢰구간 +-
confint(lm_model)
#예측치 lwr는 하한값 upr 상한값
predict(lm_model, newdata = data.frame(speed = c(10:30)), interval = "confidence")
lm_model의 예측값은 fitted()함수를 사용하여 구할 수 있고, 예측값과 실제 데이터의 값의 차이는 residuals()함수를 사용하여 다음과 같이 구할 수 있다.
위에서 만든 lm_model을 사용해 speed가 100, 150, 200일때의 dist를 예측해보자
predict(lm_model, newdata = data.frame(speed = c(100, 150, 200)))이번엔 cars의 데이터와 함께 회귀직선을 시각화해보자
#회귀직선을 시각화
with(cars, plot(speed, dist))
abline(coef(lm(dist ~ speed, data = cars)))

회귀직선과 함께 상한값, 하한값에 대한 구간또한 같이 시각화해보자.
#회귀직선을 상한, 하한값을 포함하여 시각화
speed <- seq(min(cars$speed), max(cars$speed), 0.1)
ys <- predict(lm(dist ~ speed, data = cars), newdata = data.frame(speed = speed),
interval = "confidence")
#matplot()
matplot(speed, ys, type = "l")
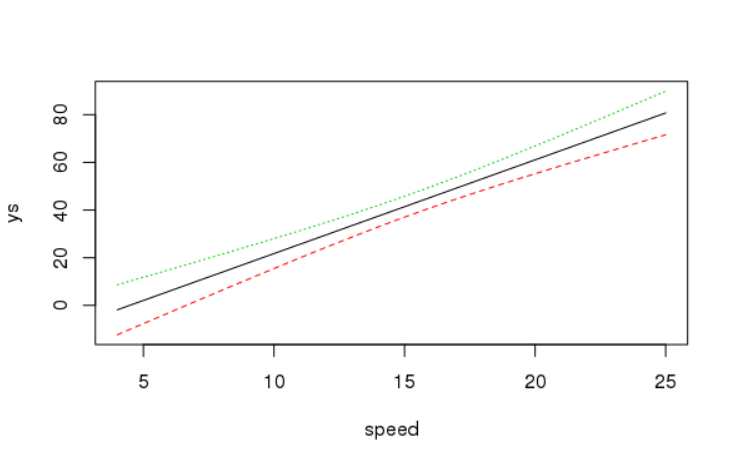
위의 그래프와 같이 speed에 따른 dist는 다음과같은 선형성을 띄며 신뢰구간은 다음과 같다고 결론을 내릴 수 있다.
다음글에서는 좀더 심화된 다중회귀분석과 분류에 대해서 알아볼 예정이다.
'Machine Learning' 카테고리의 다른 글
| K-최근접 이웃(K-Nearest Neighbor) (0) | 2019.09.25 |
|---|---|
| 뉴럴 네트워크(Neural Network) (0) | 2019.09.24 |
| 랜덤 포레스트(Random Forest) (0) | 2019.09.22 |
| 의사결정 나무(Decision Tree) (0) | 2019.09.20 |
| 로지스틱 회귀분석(Logistic Regression Analysis) (0) | 2019.09.19 |




